[笔记]非线性自适应控制器设计，对应对应DR_CAN老师的【Advanced控制理论】16

简单的自适应控制器设计，使用李雅普诺夫函数证明系统稳定性后解出对应的控制输入u，对应DR_CAN老师的【Advanced控制理论】16

其一：Advance控制理论简单的反步控制器设计

其二：从零学使用Lypunov直接法设计自适应控制器

其三：在弹性系数未知的情况下设计自适应控制器

由于博客对lateX容忍度不高，即便我开启了数学公式解析，所以想更舒服的观看的点击这里

$\dot{x}=a*{x}^{2}+u$

其中$x$是系统状态，$a$为参数，$u$为系统输入。

设置期望状态$ x}_{d}} $，状态误差为$e={{x}_{d}}-x\text{ }(2)$，控制目标为$e\to 0$

一、假设参数$a$为已知量

对(2)式求导后为：

$\dot{e}={{\dot{x}}_{d}}-\dot{x}={{\dot{x}}_{d}}-a{{x}^{2}}-u\text{ }(3)$

设计Lyapunov函数为（易知式（4）为PD（正定））：

${{V}_{(e)}}=\frac{1}{2}{{e}^{2}}\text{ }(4)$

对(4)求导并把(3)带入得：

${{\dot{V}}_{(e)}}=e\dot{e}=e({{\dot{x}}_{d}}-a{{x}^{2}}-u)\text{ }(5)$

为了满足${{\dot{V}}_{(e)}}$为ND（负定），设${{\dot{x}}_{d}}-a{{x}^{2}}-u=-ke$，

此时，${{\dot{V}}_{(e)}}=-k{{e}^{2}}$，显然此时L导数为负定，即满足系统稳定性的条件。

由此可以得出控制输入为：

$u={{\dot{x}}_{d}}-a{{x}^{2}}+ke\text{ }(6)$

仿真参考[Advance控制理论]简单的反步控制器设计

二、假设参数$a$为未知量

如一中假设参数$a$为已知量，但一般参数$a$都是未知量即一个缓慢变化的常数（例如一个机械臂需要抓取不同质量的物体，那么这个质量就是一个短时间不会变化的常数，此时$\dot{a}=0$）。

此时同样设状态误差$e={{x}_{d)-x\text{ (2)}$，

$\dot{e}={{\dot{x}}_{d}}-\dot{x}={{\dot{x}}_{d}}-a{{x}^{2}}-u\text{ }(3)$

因为参数$a$为未知量，此时需要系统估计该值，设估计值为$\widehat{a}$

估计误差为：$\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widetilde{a}}}\,=\dot{a}-\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,\text{ }$，其中$\dot{a}=0$

$\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widetilde{a}}}\,=-\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,\text{ (7)}$

此时设计Lyapunov函数(PD)为：

${{V}_{(e,a)}}=\frac{1}{2}{{e}^{2}}+\frac{1}{2}{{\widetilde{a}}^{2}}\text{ }(8)$

对(8)求导并带入(3)与(7)得：

${{\dot{V}}_{(e,a)}}=e({{\dot{x}}_{d}}-a{{x}^{2}}-u)-\widetilde{a}\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,\text{ }(9)$

为了满足(9)为负定，设$u={{\dot{x}}_{d}}-\widehat{a}{{x}^{2}}+ke\text{ }(10)$

将(10)带入(9)得：

${{\dot{V}}_{(e,a)}}=-k{{e}^{2}}-\widetilde{a}(e{{x}^{2}}+\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,)\text{ }(11)$

易知，$-k{{e}^{2}}$为ND，若令$\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,=-e{{x}^{2}}$，此时${{\dot{V}}_{(e,a)}}=-k{{e}^{2}}$为NSD(半负定)。

引入引理1：假设

①$V\ge 0$

②$\dot{V}<-g(t)\text{ }(g(t)\ge 0)$且$\dot{g}(t)\in {{L}_{\infty }}$

那么$g(t)$有界，即$\underset{t\to \infty }{\mathop{\lim }}\,g(t)=0$

由引理1知，式(11)在设$\overset{\text{ }\!\!\cdot\!\!\text{ }}{\mathop{\widehat{a}}}\,=-e{{x}^{2}}$情况下满足李雅普诺夫稳定条件。

$\widehat{a}=-\int_{0}^{t}{e{{x}^{2}}dt}$

最终得控制输入$u$为：

$u={{\dot{x}}_{d}}+{{x}^{2}}\int_{0}^{t}{e{{x}^{2}}dt}+ke\text{ }(12)$

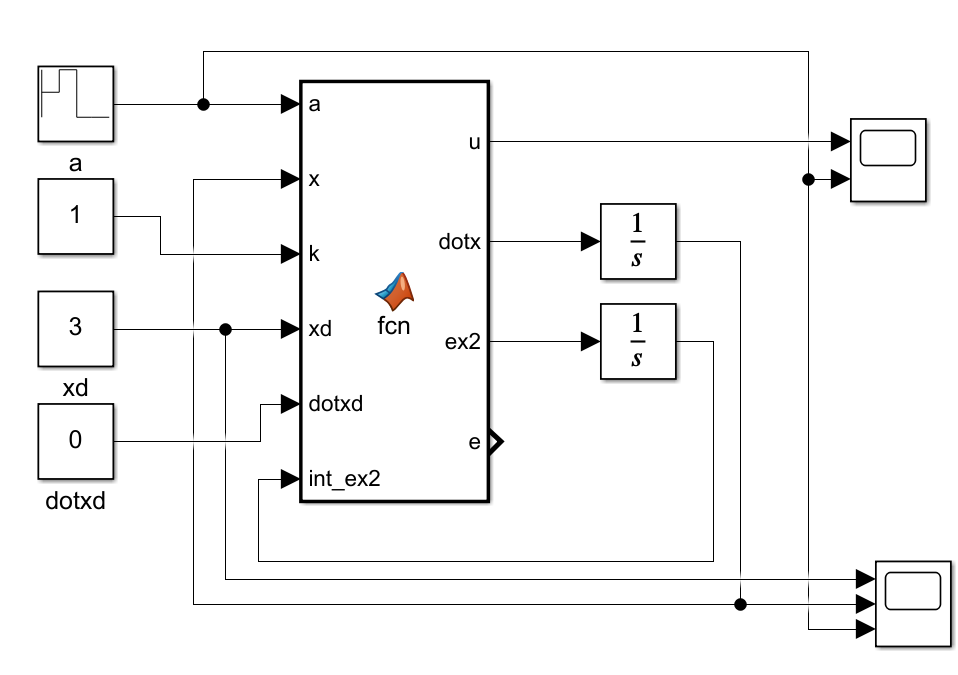
Matlab/Simulink仿真为：

function [u, dotx, ex2, e] = fcn(a, x, k, xd, dotxd, int_ex2)
%#codegen
e = xd - x;
ex2 = e*x^2;
u = dotxd + int_ex2*x^2 + k*e;
dotx = a*x^2 + u;

在目标状态$x_d$不变得情况下，未知参数$a$的改变会使控制输入经历一段时间的调整后$e\to 0$。

在不知道参数$a$的情况下，$\widehat{a}$可以很好的估计参数值。

本文作者：sheetung

本文链接：https://cutech.space/archives/adcontrol16.html

版权声明：转载时须注明出处（包括原作者和文章链接）及本声明